Elon Musk believes we live in a simulation. His argument goes:
“If you assume any rate of improvement at all, games will eventually be indistinguishable from reality” — Elon Musk, Founder PayPal, Tesla, SpaceX
What are the chances someone beat us to it? With the potential for many simulated realities, the odds are low we’re in the ‘real’ one. What does this have to do with Bayesian Statistics?
Bayesian Statistics
Statistics is about inferring something about how the world works, so we can make better decisions. We care about what causes sales for our business, so we commonly build statistical models to look at historic data and figure out what’s causing the peaks and dips. Once we have a model that accurately predicts past data, we can use it to plan out future scenarios, for example what our Marketing Return on Investment (MROI) would be, if we shifted more budget into Facebook Ads.
Assume there are infinite universes, each with a different probability of generating the data we observed. Bayesian Statistics is just a method for figuring out which of those universes we’re most likely to be in. If the universes where Facebook Ads has around a $5 Cost per Acquisition (CPA), are the ones that best match to our data, it’s likely Facebook really does drive new customers for five bucks.
You might be tempted to apply brute force and simulate all possible universes, and pick the ones whose predictions best match our observations. But all possible universes is, well, a lot of universes, and this leads to two big problems. First, your computer is going to have to do a lot of work, much of it spent playing out totally implausible scenarios that should never have been considered in the first place. Second, out of pure chance, there are likely to be some fairly whacky combinations of parameters that fit the data pretty well. What do you do with them?
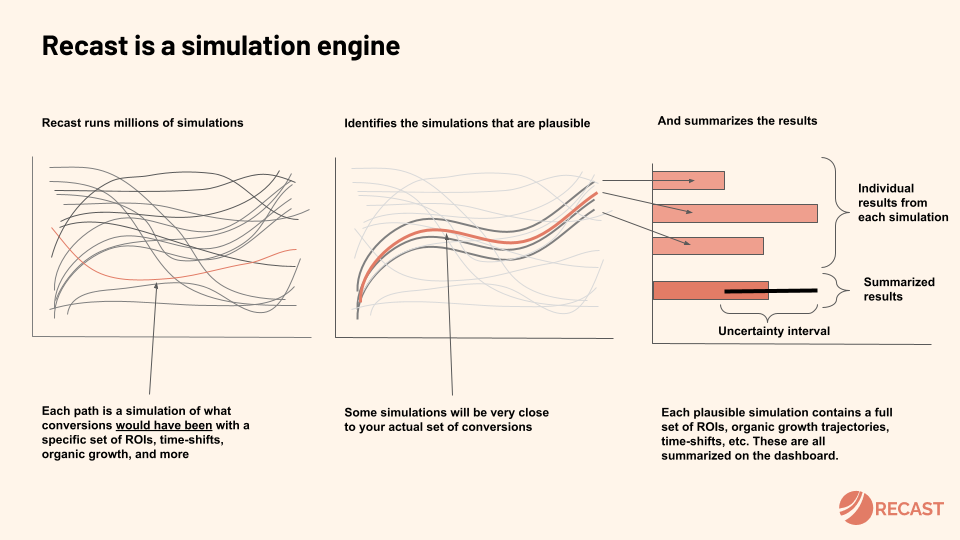
Modern Bayesian statistics can be thought of as doing two things: first, narrowing down the search by layering in your existing assumptions, and second, efficiently running simulations and choosing the ones that best fit the data. Think of this as similar to the game Battleship: first you want to choose a point that’s actually on the board, and then once you hit a ship, it makes sense to cluster your guesses around that spot until you’ve sunk it.
Some reasonable assumptions (or priors) might be as follows:
- Facebook Ad spend had a positive impact on sales
- Facebook ROI is likely to be somewhere between 1x and 3x
- As you spend more on Facebook you see diminishing returns
- Facebook Ads have an adstock effect (delayed impact over time)
This allows to exclude obviously implausible results like a -10x ROI (spend a dollar, lose $10 in sales!?), or the ability to spend a trillion dollars in a day without saturating the channel.
But even with this much smaller search space, we still have a major computational problem. Assume we had thirty channels, each with three parameters (ROI, saturation, and shift), and to make it simple — assume that each of the parameters could either be “low” or “high”. That would still be 2^(30*3) simulations to run to cover all possibilities.
It’s better than infinite, but not by much.
Hamiltonian Monte Carlo
Solving this problem is the magic of Hamiltonian Monte Carlo, which combines the steps of running the simulations according to your assumptions and choosing the ones that fit the data. It does this by creating a landscape that defines where good simulations are more or less likely to be found, and uses techniques from physics to travel around it.
The mechanism is similar to throwing a ball into mountainous terrain (the probability distribution), then watching it roll downhill. The deepest part of a valley is the highest probability range for a parameter, and the mountains represent less promising places to look. We may have seen from the data so far that Facebook Ads most likely drives sales for between $4.50 and $5.50, so we throw our next ball in that valley, and learn a little bit more about its shape. There’s also a clever technique employed – giving the ball momentum so it doesn’t get stuck – so it doesn’t waste all its time in a ditch when the Grand Canyon is next door! Don’t worry – you don’t need to know the math to benefit from it.
Even though Bayes’ theorem is two centuries old, it powers the Hamiltonian Monte Carlo method under the hood, delivering highly accurate and intuitive results. Because we get a range of potential outcomes back rather than a fixed number, we can tell something about the certainty of each parameter, which is very useful in practice. Compared to Frequentist techniques like Ordinary Least Squares Regression, it uses a lot more computational power, but gives us much more flexibility in return.
Why Bayesian?
The ability to set prior assumptions about how a marketing channel works is an unfair advantage. Bayesian Marketing Mix Models (MMM) let us take into account the expertise of people who know and run the business, letting us get to more plausible and consistent results. This feature offers essential protection against bad results, which is important when you want your model to update in automatically, in real-time, without human intervention. That’s why the latest generation of data-driven marketing teams at companies like HelloFresh, MasterClass, Asana, Away and Harry’s (where my cofounder led the Marketing Science team before founding Recast), as well as researchers at Google, are betting on Bayesian.



