Bayesian Marketing
Mix Modeling

The privacy-friendly modeling technique from the 1960s being modernized and automated by Google, Facebook, and Recast.

Bayesian Marketing Mix Modeling

understand how it works

Marketing Optimization

allocate your budget to
maximize sale

Incremental ROMI

calculating your true marketing
performance

Diminishing Returns

predicting when channels hit
saturation

Adstock Rates

the lagged effect of ad spend
over time

Seasonality

the impact of holidays and
general market trends

Marketing Mix Modeling (MMM) has been around since the 1960s, used by CPG brands to help them allocate their marketing budgets across different marketing channels. Bayesian statistics have been around far longer – Bayes theorem was published in the 1760s! So you might be surprised to find that Bayesian Marketing Mix Modeling is now at the forefront of how marketing attribution is done by modern consumer brands like Away, HelloFresh, MasterClass, Truebill, and Harry’s (where I led the marketing science team before founding Recast). This statistical modeling technique is gaining in popularity as marketing teams graduate from Facebook ads to TV, and from last click attribution to privacy-friendly methods. With Google publishing papers on the topic and Facebook releasing an open-source tool, and companies (like Recast) offering MMM-as-a-service, these methods are more accessible than ever.

Rather than an expensive 3 month project done once a year, it’s now possible to automate marketing mix modeling, with data pipelines, daily model updates, and always-on recommendations. When you’re no longer building your model manually, you need safeguards in place to ensure your model makes sense, is accurate, and consistent with what you know about your business. This is something that can only be done at scale with Bayesian Statistics, specifically Markov Chain Monte Carlo (MCMC) sampling, which is flexible enough to allow us to incorporate prior domain knowledge. However this process can be complex, so we’re sharing these best practices for building a Bayesian Regression Model.

Our Team

Tom holds a master’s degree from the London School of Economics and an MBA from Wharton. Prior to co-founding Recast he built a quantitative market research firm consulting for clients such as Amazon, McKinsey and Nike.

Tom

Co-Founder of Recast

Michael is a trained econometrician with a background in healthcare and environmental economics. He previously built the marketing science team at men’s grooming brand Harry’s before co-founding Recast.

Michael

Co-Founder of Recast

Marketing
Optimization

“I know half of my marketing spend is wasted, the trouble is I don’t know which half” – John Wannamaker

Why do we care about measuring the impact of our marketing spend at all? The whole reason we do are doing this is to be able to optimize our marketing budget. That is, we can improve our business performance by eliminating wasted or inefficient marketing spend and doubling down in our best performing marketing channels.

The age-old problem in marketing has always been one of measurement. Once we can identify which channels or methods are working for the business, we can improve our marketing profitability — that’s the end goal: improving the profitability of our business by better allocating our marketing dollars to the channels and methods that are going to best help the business.

Incremental Return
on Marketing Investment
(ROMI)

Incremental ROMI (return on marketing investment) is the amount of sales that each channel is truly contributing to our business.

Incrementality is the most important but least understood term when discussing marketing effectiveness. When we talk about incrementality, we mean the amount of “lift” driven by a marketing channel over and above the amount of sales that we would have gotten anyway.

Unfortunately, this notion of incrementality is not as easy to measure as it may seem — the problem is that from your business’s perspective it’s very difficultto tell:

Which customers saw an ad but would have purchased anyway
Which customers saw multiple ads but were only convinced by one of them

In today’s modern advertising world, programmatic advertisers like Facebook are very good at showing your ads to the people most likely to purchase. However, it’s very difficult to tell if a Facebook ad convinced someone to purchase or simply showed an ad to someone already very likely to buy.

When we say “incrementality” we mean: how many additional customers will you get for additional dollars spent in a marketing channel.

Diminishing
Returns
(Saturation Rates)

Let’s say you find a channel with a high incremental ROMI. How much more should you spend into that channel? 10% more? 50% more? 10 times as much?

The answer that to question will be determined by how quickly the channel’s incrementality decreases as you add more spend. We know that at some point, you will see diminishing returns. If this weren’t the case, you’d quickly be making unworkable recommendations, like piling all of your marketing budget into a single channel, or spending practically infinite sums.

But why does performance diminish as you spend more?

A big reason is that you start to reach consumers that are less and less relevant to your business. In order to bill you more, platforms have to show your ads to more people, and as they widen their targeting criteria out from the most attractive consumers, the performance of your ads will decay.

A second reason is that you start to over-saturate the people that are seeing your ads. There will come a point when yet-another-ad from the same business simply isn’t increasing aided or unaided awareness, consideration, or anything.

Estimating the diminishing returns for each channel is one of the most challenging components of a Bayesian MMM, but also one of the most critical. Getting it wrong can leave money on the table with underspent marketing channels, or wasting lots of money by overspending!

Recast uses the Hill Function to model saturation effects. In our variation, it takes two parameters: beta, and kappa. Beta can be thought of as the base-level efficiency of the channel, and kappa as the point when the channel’s efficiency starts to decline. At any given level of spend, a channel’s ROI will be

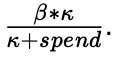
Adstock Rates
(Carryover Effect)

If you spend a dollar today in a marketing channel, you expect it to drive some incremental revenue. But when?

For some performance-based lower-funnel channels, you may see all that revenue on that same day. But even with these channels, some customers will forget they were in the middle of making a purchase and come back the next day — so some of that incremental revenue will be slightly delayed from the time you spent the money.

For other channels, there are much longer delays. Upper-funnel channels focused more on awareness and brand recognition may take time to have their effect, first building awareness and trust, which only later contribute to a conversion at a point of purchase. Channels like direct mail or podcasts may even take time to be distributed. Direct mail has to actually go through the mail—and then be opened! People listen to podcasts well after they are released.

There may be other reasons for a delay. If you run a freemium product and you’re measuring paid conversions, there may be a period while the customer is trialing the product before they open their wallet.

Marketers call this time delay between the cause and effect the “adstock” effect. Originally this was so-called because new advertising contributed to the “stock” of advertising as perceived by the consumer, decaying at roughly the rate that memories fade.

An ad for Coca- Cola may have its effect later than when it was seen because the consumer still had a memory (perhaps subconscious) of the ad. This is still very much a reason (see the sentence on upper-funnel channels above). But it’s not the only one, and marketers today generally accept that different channels may have very different adstock effects—or delays between when the money is spent and when the returns start rolling in. Estimating this delay is core to the challenge of building an MMM, since it’s the chain that links cause and effect.

In Recast, we use the density of a negative-binomial distribution to model the shape of the adstock effect. The negative-binomial distribution is defined on non-negative integer values, which is perfect when we’re using days to index time from the date of spend, and as a probability distribution, its density values will add up to one. Finally, it can accommodate a range of shapes that map to our intuitions about how the effect of spend should be distributed over time.

Adstocks in R

library (tidyverse)
n_samples = 100
mean_shift = runif(n_samples, 0.5, 10)
concentration = runif(n_samples, 0.1, 2)
timesteps = 20

map_dfc (1:n_samples, function(i) {
dnbinom(0:(timesteps-1), mu = mean_shift[i], size = mean_shift[i])
}) %>%
mutate(days_since_spend = 0:(timesteps-1)) %>%
gather(k, v, -days_since_spend) %>%
ggplot() +
aes(x = days_since_spend, y = v, group = k) +
geom_line(col = scales::alpha('black', 0.5)) +
scale_y_continuous("Percent of effect on this day", label = scales::percent) +
labs(x = "Days since spend", title = "Examples of adstock effect") +
theme_bw()

Seasonality
and Holidays

Almost every business has certain times of year — or even certain days of the year — when it tends to do better or worse.

Companies that cater to families preparing their kids for another school year will see their sales spike in August.

Companies focused on self-improvement or entrepreneurship will see peaksof activity right after the New Year. And consumer brands may go from red to black on Black Friday (so-called because that’s—at least historically— when many retailers actually did start to make money for the first time in the year).

So each business has natural peaks and valleys scattered across the calendar. This is what is meant by seasonality. The question for the modeler is: how do you deal with it?

It is common to include control variables that attempt to fit this seasonal cycle. The modeler could extract those terms, plot them as a line graph, and say — convincingly — that this is what seasons “look like” for the business. The problem is that this tends to conceal—or even disguise—important facts about what marketers ought to do.

Including a seasonal term could lead the modeler to say “controlling for the fact that it’s August, our marketing spend is not very effective” for a back-to-school brand, recommending that they pull back on their investment. This would come at the time when marketing spend was most effective because it’s August. Parents are buying supplies and you have the opportunity to speak to them right when they’re looking for your products.

So seasonality is important, but must be handled with nuance. At Recast, we model seasonality but we don’t control for it. We model seasonality by layering in the assumption (and since we’re Bayesian, this is accomplished through our priors), that “today is like a year ago”. That is, if every August, your marketing spend seems to be really effective, the model is going to have a going-in assumption of effective marketing spend the next time August rolls around.

This has the desired effect of building in the idea that sales should go up every August, but also transmitting the correct recommendations. In this case, to spend more!

Marketing Mix
Modeling in R

We’re on a mission to make what we do more accessible to marketers who want to be more technical and data-driven – we can only work with so many clients! We use the Bayesian MCMC library Stan at Recast (in fact, we have several core Stan developers on the team!) so we put together the following script.

bayesian_mmm_r.ipynb

Make a copy of the Google Colab script above and you can run this code yourself,
or modify it for your own business. You can also copy the code across to R Studio
if that’s what you prefer. Below is a description of what the code does.

install.packages("rstan")
library(rstan)
options(mc.cores = parallel::detectCores())

First we install and load the rstan library, and set the number of cores for parallel
processing, by detecting how many your machine has available.

model <- "
functions {
  vector adstock(vector x, int n_timesteps, real rate) {
  vector[n_timesteps] out = x;
    for (i in 1 : n_timesteps) {
     if (i == 1) {
       out[i] = out[i] * rate ;
     } else {
       out[i] = out[i] * rate + (1-rate) * out[i-1];
     }
}
    return (out);
  }
}

data {
  int n_timesteps;
  int n_channels;
  matrix[n_timesteps, n_channels] spend;
  vector[n_timesteps] depvar;
}

parameters {
  real<lower=0> intercept;
  real<lower=0> sigma;
  vector<lower=0>[n_channels] betas;
  vector[n_channels] adstock_rates_raw;
  vector<lower=0>[n_channels] kappas; // half-saturation point. How to set?
}

transformed parameters {
  vector[n_timesteps] predicted = rep_vector(0, n_timesteps);
  vector[n_channels] adstock_rates = inv_logit(adstock_rates_raw);
  matrix[n_timesteps, n_channels] rois;
  matrix[n_timesteps, n_channels] adstocked_spend;

  predicted = rep_vector(intercept, n_timesteps);
  for(i in 1:n_channels) {
    adstocked_spend[, i] = adstock(spend[, i], n_timesteps, adstock_rates[i]);
    for (j in 1:n_timesteps) {
      rois[j, i] = betas[i] * kappas[i] / (adstocked_spend[j, i] + kappas[i]);
    }
    predicted += rois[, i] .* adstocked_spend[,i];
  }
}

model {
  intercept ~ normal(0,1);
  betas ~ normal(0,1);
  adstock_rates_raw ~ normal(0,1);
  kappas ~ normal(0,1);
  sigma ~ exponential(1);
  depvar ~ normal(predicted, sigma);
} "

We set the model code in Stan, which is it’s own language. This creates a function
for our adstocks, creates the parameters for our model, handles transformations
for saturation and adstocks, then builds the model.

m <- rstan::stan_model(model_code = model)

adstock <- function(x, rate) {
  for (i in 1:length(x)) {
     if (i == 1) {
       x[i] <- x[i] * rate
     } else {
       x[i] <- x[i] * rate + (1-rate) * x[i-1];
} }
return (x) }

time <- 500

spend <- matrix(, ncol=2, nrow= time)
spend[,1] <- abs(cumsum(rnorm(time,)))

spend[,2] <- abs(cumsum(rnorm(time,)))

true_betas <- c(0.5, 1.5)
true_adstocks <- c(0.1, 0.35)
true_kappas <- c(0.4, 0.99)
true_intercept <- 3

as_spend <- matrix(, nrow=time, ncol=2)
rois <- as_spend

for (i in 1:ncol(spend)) {
  as_spend[,i] <- adstock(spend[,i], true_adstocks[i])
  rois[,i] <- true_betas[i] * true_kappas[i] / (as_spend[,i] + true_kappas[i])
}
dv <- rep(true_intercept, time)

for (i in 1:ncol(spend)) {
  dv <- dv + as_spend[,i] * rois[,i]
}

dv <- dv + rnorm(time, 0, 0.01)

stan_data <- list(n_timesteps = time, n_channels = 2, spend = spend, depvar = dv)

Now we’re back in R code, so we feed the stan code into the rstan library,
then generate our data based on the true model parameters we chose for this
illustration.

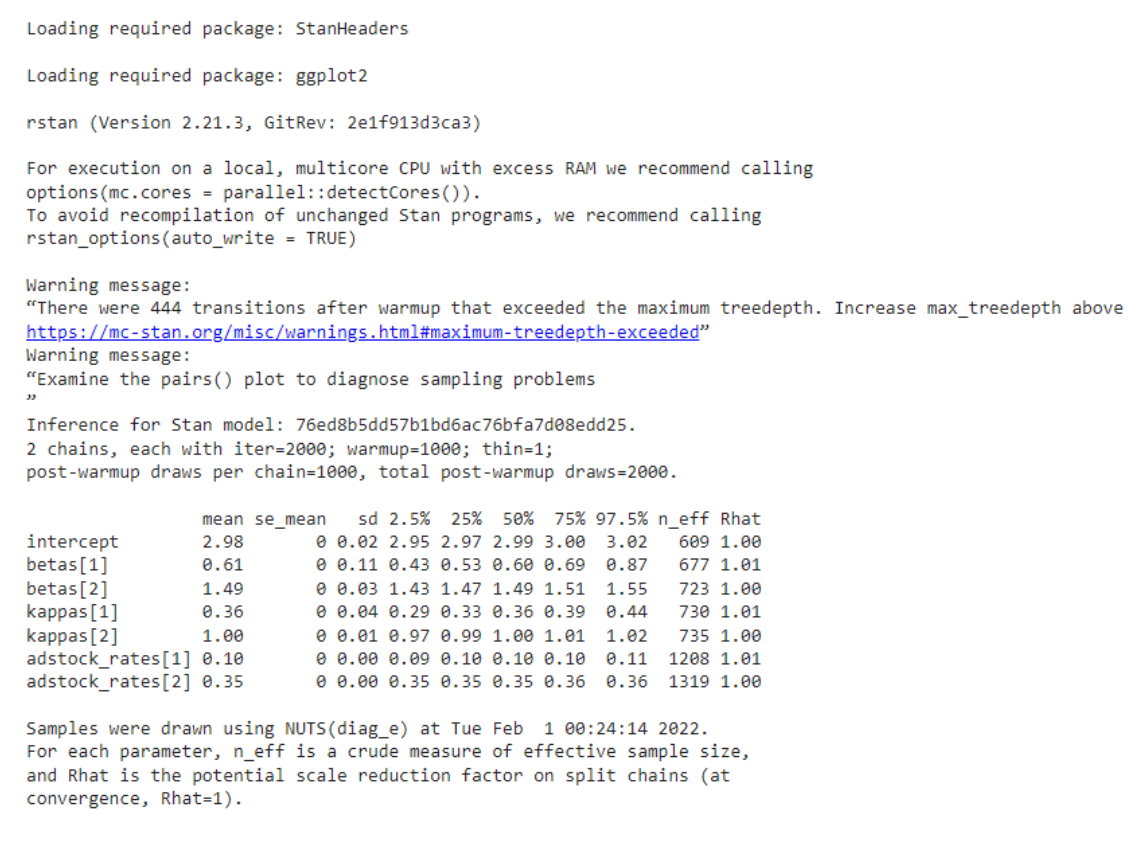
fit <- sampling(m, data=stan_data, chains = 2, cores = 2)

print(fit, pars=c("intercept", "betas", "kappas", "adstock_rates"))

Finally we fit the model to the data, and print out the model output, which looks
like this:

Bayesian Marketing
Mix Modeling